算法

LCA之Tarjan算法

寻找最近公共祖先有两种效率高的算法，一种是离线算法Tarjan算法，用户输入所有查询，算法给出所有查询结果，算法在运行的时候就已经知道用户的所有查询了，时间复杂度为O(nlogn)。另外一种是在线算法DFS+ST算法，算法运行不需要知道用户的输入，每一次查询可以在常数时间内给出结果。时间复杂度为DFS->O(n), ST->O(nlogn)。这里主要讲一下Tarjan算法。

Tarjan算法是DFS搜索和并查集的思想的结合，深度搜索每一个节点，对于当前的节点x，将其看做一个新的集合，并将其作为该集合的代表，查询处理与该节点有关的查询，接着递归遍历该节点的所有子节点，在遍历完所有子节点后，将该集合与root集合合并，也就是并查集的Union操作。在查询的过程中还可以使用路径压缩的方法来提高查询效率。例如：如果有查询（a, b）,那么当遍历到a节点的时候，如果b节点已经遍历过了，那么分两种情况，如果b在另外一个子树上，那么查找b的时候，b所在的结合的代表就是a和b的最近公共祖先。如果b不在另一颗子树上，而是与a同在一颗子树，那么此时的b就是最近公共祖先。这也就是为什么在需要在遍历完节点的所有子节点后才可以将当前节点与root合并的原因。

例子：Nearest Common Ancestors

Description

A rooted tree is a well-known data structure in computer science and engineering. An example is shown below:

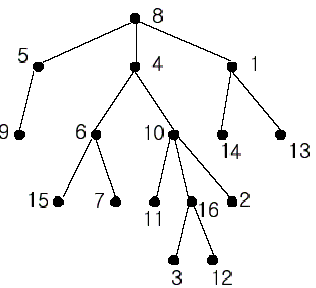
In the figure, each node is labeled with an integer from {1, 2,…,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.

For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.

Write a program that finds the nearest common ancestor of two distinct nodes in a tree.

Input

The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case starts with a line containing an integer N , the number of nodes in a tree, 2<=N<=10,000. The nodes are labeled with integers 1, 2,…, N. Each of the next N -1 lines contains a pair of integers that represent an edge –the first integer is the parent node of the second integer. Note that a tree with N nodes has exactly N - 1 edges. The last line of each test case contains two distinct integers whose nearest common ancestor is to be computed.
Output

Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.

Sample Input

2
16
1 14
8 5
10 16
5 9
4 6
8 4
4 10
1 13
6 15
10 11
6 7
10 2
16 3
8 1
16 12
16 7
5
2 3
3 4
3 1
1 5
3 5

Sample Output

4
3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
#include<stdio.h>
#include<vector>
#include<string.h>
using namespace std;
#define Size 11111  //节点个数

vector<int> node[Size],que[Size];
int n,pare[Size],anse[Size],in[Size],rank[Size];

int vis[Size];
void init()
{
	int i;
	for(i=1;i<=n;i++)
	{
		node[i].clear();
		que[i].clear();
		rank[i]=1;
		pare[i]=i;///
	}
	memset(vis,0,sizeof(vis));
	memset(in,0,sizeof(in));
	memset(anse,0,sizeof(anse));

}

int find(int nd)
{
	return pare[nd]==nd?nd:pare[nd]=find(pare[nd]);
}
int Union(int nd1,int nd2)
{
	int a=find(nd1);
	int b=find(nd2);
	if(a==b) return 0;
	else if(rank[a]<=rank[b])
	{
		pare[a]=b;
		rank[b]+=rank[a];
	}
	else
	{
		pare[b]=a;
		rank[a]+=rank[b];
	}
	return 1;

}

void LCA(int root)
{
	int i,sz;
	anse[root]=root;//首先自成一个集合
	sz=node[root].size();
	for(i=0;i<sz;i++)
	{
		LCA(node[root][i]);//递归子树
		Union(root,node[root][i]);//将子树和root并到一块
		anse[find(node[root][i])]=root;//修改子树的祖先也指向root
	}
	vis[root]=1;
	sz=que[root].size();
	for(i=0;i<sz;i++){
      if(vis[que[root][i]]){

        //root和que[root][i]所表示的值的最近公共祖先
				printf("%d\n",anse[find(que[root][i])]);
				return ;
			}
	}
     return ;
}

int main()
{
	int cas,i;
	scanf("%d",&cas);
	while(cas--)
	{
		int s,e;
		scanf("%d",&n);
		init();
		for(i=0;i<n-1;i++)
		{
			scanf("%d %d",&s,&e);
			if(s!=e)
			{
			    node[s].push_back(e);
			   // node[e].push_back(s);
				in[e]++;
			}
		}
		scanf("%d %d",&s,&e);
		que[s].push_back(e);
		que[e].push_back(s);
		for(i=1;i<=n;i++)  if(in[i]==0) break;//寻找根节点
	  //	printf("root=%d\n",i);
		LCA(i);
	}
	return 0;
}

代码转载自这里

例子：CD操作

Problem Description

在Windows下我们可以通过cmd运行DOS的部分功能，其中CD是一条很有意思的命令，通过CD操作，我们可以改变当前目录。
这里我们简化一下问题，假设只有一个根目录，CD操作也只有两种方式： 　　

  1. CD 当前目录名...\目标目录名 (中间可以包含若干目录，保证目标目录通过绝对路径可达)
  2. CD .. (返回当前目录的上级目录)
    　　
    现在给出当前目录和一个目标目录，请问最少需要几次CD操作才能将当前目录变成目标目录？
Input

输入数据第一行包含一个整数T(T<=20)，表示样例个数；
每个样例首先一行是两个整数N和M(1<=N,M<=100000)，表示有N个目录和M个询问；
接下来N-1行每行两个目录名A B(目录名是只含有数字或字母，长度小于40的字符串)，表示A的父目录是B。
最后M行每行两个目录名A B，表示询问将当前目录从A变成B最少要多少次CD操作。
数据保证合法，一定存在一个根目录，每个目录都能从根目录访问到。

Output

请输出每次询问的结果，每个查询的输出占一行。

Sample Input

2
3 1
B A
C A
B C

3 2
B A
C B
A C
C A

Sample Output

2
1
2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
//思路：

//　　求出a和b的最近公共祖先,然后分4种情况讨论

//　　①. a和b有一个公共祖先c，则用 c时间戳-a的时间戳+1(1步可以直接从c到b)

//　　②. a是b的祖先，则只用1步就可以到达b点

//　　③. b是a的祖先，则用a的时间戳-b的时间戳

//　　④. a和b是同一个点，则答案是0

#include<stdio.h>
#include<vector>
#include<string.h>
#include<map>
#include<math.h>
#include<string>
using namespace std;
#define Size 111111  //节点个数
struct Query
{
    int nd,id;
}temp;
struct out
{
    int s,e;
}out[Size];
vector<int> node[Size];
vector<struct Query>que[Size];
int n,m,pare[Size],ance[Size],in[Size],rank[Size],dis[Size],ans[Size],vis[Size];
map<string,int>mp;
void init()
{
	int i;
	for(i=1;i<=n;i++)
	{
		node[i].clear();
		que[i].clear();
		rank[i]=1;
		pare[i]=i;///
	}
	memset(vis,0,sizeof(vis));
	memset(in,0,sizeof(in));
	memset(ance,0,sizeof(ance));
	memset(dis,0,sizeof(dis));
	mp.clear();
}
int aabs(int aa)
{
     if(aa>0) return aa;
     else return -aa;
}
int find(int nd)//并查集操作  不解释
{
	return pare[nd]==nd?nd:pare[nd]=find(pare[nd]);
}
int Union(int nd1,int nd2)//并查集操作  不解释
{
	int a=find(nd1);
	int b=find(nd2);
	if(a==b) return 0;
	else if(rank[a]<=rank[b])
	{
		pare[a]=b;
		rank[b]+=rank[a];
	}
	else
	{
		pare[b]=a;
		rank[a]+=rank[b];
	}
	return 1;
}
void LCA(int root,int num)
{
	int i,sz;
	ance[root]=root;//首先自成一个集合
	dis[root]=num;
	sz=node[root].size();
	for(i=0;i<sz;i++)
	{
		   LCA(node[root][i],num+1);//递归子树
		   Union(root,node[root][i]);//将子树和root并到一块
		 ance[find(node[root][i])]=root;//修改子树的祖先也指向root
	}
	vis[root]=1;
	sz=que[root].size();
	for(i=0;i<sz;i++)
	{
	    int nd1,nd2,idx,ancestor;
	    nd1=root;nd2=que[root][i].nd;idx=que[root][i].id;
            if(vis[nd2])
			{
                  ans[idx]=ance[find(nd2)];
			}
	}
     return ;
}

int main()
{
	int cas,i;
	scanf("%d",&cas);
	while(cas--)
	{
		char  ss[100],ee[100];
		int s,e,cnt=1;
		scanf("%d %d",&n,&m);
		init();
		for(i=0;i<n-1;i++)
		{
			scanf("%s %s",ee,ss);
			if(mp.find(ss)==mp.end())
            {
                 s=cnt;mp[ss]=cnt++;
            }
            else s=mp[ss];
			if(mp.find(ee)==mp.end())
            {
                e=cnt;mp[ee]=cnt++;
            }
            else  e=mp[ee];
			if(s!=e)
			{
			    node[s].push_back(e);
				in[e]++;
			}
		}
		for(i=0;i<m;i++)
        {
		   scanf("%s %s",ss,ee);
		   s=mp[ss];e=mp[ee];
		   out[i].s=s;out[i].e=e;
		   temp.nd=e;temp.id=i;
		   que[s].push_back(temp);
		   temp.nd=s;temp.id=i;
		   que[e].push_back(temp);
        }
		for(i=1;i<=n;i++)  if(in[i]==0) break;//寻找根节点
		LCA(i,0);
		for(i=0;i<m;i++)
        {
            if(out[i].s==out[i].e)
                printf("0\n");
            else
                if(out[i].s==ans[i])
                      printf("1\n");
            else if(out[i].e==ans[i])
                printf("%d\n",dis[out[i].s]-dis[ans[i]]);
            else
            printf("%d\n",dis[out[i].s]-dis[ans[i]]+1);
        }
	}
	return 0;
}

代码转载自这里

例子：Connections between cities

Problem Description

After World War X, a lot of cities have been seriously damaged, and we need to rebuild those cities. However, some materials needed can only be produced in certain places. So we need to transport these materials from city to city. For most of roads had been totally destroyed during the war, there might be no path between two cities, no circle exists as well.
Now, your task comes. After giving you the condition of the roads, we want to know if there exists a path between any two cities. If the answer is yes, output the shortest path between them.

Input

Input consists of multiple problem instances.For each instance, first line contains three integers n, m and c, 2<=n<=10000, 0<=m<10000, 1<=c<=1000000. n represents the number of cities numbered from 1 to n. Following m lines, each line has three integers i, j and k, represent a road between city i and city j, with length k. Last c lines, two integers i, j each line, indicates a query of city i and city j.

Output

For each problem instance, one line for each query. If no path between two cities, output “Not connected”, otherwise output the length of the shortest path between them.

Sample Input

5 3 2
1 3 2
2 4 3
5 2 3
1 4
4 5

Sample Output

Not connected
6

Hint

Huge input, scanf recommended.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
#include<stdio.h>
#include<string.h>
#include<vector>
using namespace std;
#define Size  11111
struct Edge
{
    int y,val;
}temp;
struct Query
{
    int y,id;
}mid;
int pare[Size],ance[Size],vis[Size],dis[Size],rank[Size],ans[1000000+100],n,m,c,tree[Size];
vector<struct Query>que[Size];
vector<struct Edge>node[Size];
void init()
{
    int i;
    for(i=0;i<=n;i++)
    {
        vis[i]=0;
        pare[i]=i;
        dis[i]=0;
        rank[i]=1;
        que[i].clear();
        node[i].clear();
    }
    memset(ans,-1,sizeof(ans));
}
int find(int x)
{
    return pare[x]==x?x:pare[x]=find(pare[x]);
}
/*
void Union(int x,int y)
{
x=find(x);
y=find(y);
if(x!=y)
{
if(rank[x]>rank[y])
{
rank[x]+=rank[y];
pare[y]=x;
}
else
{
rank[y]+=rank[x];
pare[x]=y;
}
}
}
*/
void LCA(int root,int d,int k)//k表示是以第k个点作为根的树
{
    int i,sz,nd1,nd2;
    vis[root]=1; //已经遍历过的点 要标记一下 不要
    tree[root]=k;dis[root]=d;
    // ance[root]=root;
    sz=node[root].size();
    for(i=0;i<sz;i++)
    {
        nd2=node[root][i].y;
        if(!vis[nd2])
        {
            LCA(nd2,d+node[root][i].val,k);
            // Union(node[root][i].y,root);//用带rank的幷查集操作答案不对 不知道why
            int w=find(nd2),m=find(root);
            if(w!=m)
            {
               pare[w]=m;//这样才对
            }
            //ance[find(node[root][i].y)]=root;
        }
    }
    sz=que[root].size();
    for(i=0;i<sz;i++)
    {
        nd1=root;
        nd2=que[root][i].y;
        if(vis[nd2]&&tree[nd1]==tree[nd2])//如果 nd1 nd2 的跟是同一个点 则是同一棵树上的
        {
            ans[que[root][i].id]=dis[nd1]+dis[nd2]-2*dis[find(nd2)];
        }
    }
}
int main()
{
    int i,j,x,y,val;
    while(scanf("%d %d %d",&n,&m,&c)!=EOF)
    {
        init();
        for(i=0;i<m;i++)
        {
            scanf("%d %d %d",&x,&y,&val);
            if(x!=y)
            {
                temp.y=y;temp.val=val;
                node[x].push_back(temp);
                temp.y=x;
                node[y].push_back(temp);//路是2个方向都可以通行的
            }
        }
        for(i=0;i<c;i++)
        {
            scanf("%d %d",&x,&y);
            mid.id=i;
            mid.y=y;
            que[x].push_back(mid);
            mid.y=x;
            que[y].push_back(mid);
        }
        for(i=1;i<=n;i++)
        {
            LCA(i,0,i);//以每一个节点作为根节点去深度搜索  找出每个点作为根的所有最近公共祖先
        }
        for(i=0;i<c;i++)
        {
            if(ans[i]==-1)
                printf("Not connected\n");
            else
                printf("%d\n",ans[i]);
        }
    }
    return 0;
}
//本题给的是一个森林 而不是一颗树，由于在加入边的时候，我们让2个方向都能走这样就形成了一个强连通的快，
//对于这个快来说，不管从快上那点出发 都可以遍历这个快上的所有的点，且相对距离是一样的

代码转载自这里