算法

LCA之DFS+ST算法

DFS+ST算法可以在线的查询两个节点的最近公共祖先。由于任意两点的最近公共祖先必定在这两点的最短路径上，所以也可以根据这个特性来查找任意两点的最近路径。
DFS：深度优先遍历树的每一个节点，用数组deep按照遍历顺序记录下每一个节点的深度，另外需要记录每一个节点在数组中所对应的第一个出现的下标。
ST：有了深度数组，利用ST算法计算每一个偶数段的区间的最小深度的下标。
对于每一个查询(a, b), 先获得a和b在深度数组中第一次出现的下标firsta和firstb，接下来就是求出在深度数组中下标从firsta到firstb的最小值的下标，改下标对应的节点就是最近公共祖先。求最小值的下标ST算法可以在线的以常数的时间给出。如果需要求出两点之前的最短路径长度，那么可以直接的deep[a]+deep[b]-2*deep[最近公共祖先下标]。

例题：

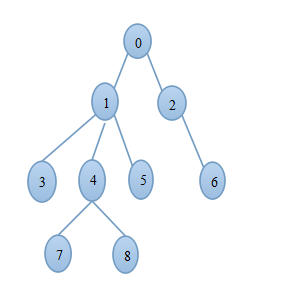
采用DFS遍历整棵树，得到以下数据：

（1）遍历序列p：0　　1　　3　　1　　4　　7　　4　　8　　4　　1　　5　　1　　0　　2　　6　　2　　0

（2）各节点的深度序列　　　　　　　 depth: 0　　1　　 1　　 2　　 2　　2　　 2　　 3　　3

（3）各节点在序列p中首次出现的位置序列pos: 0　　1　　13　　2　　4　　10　　14　　5　　7

使用ST算法，假设现在我们要求节点7和5的最短路径，我们可以这样做：

（1）首先，从pos序列中获得节点7和节点5在p序列中第一次出现的位置分别为：pos[7] = 5, pos[5] = 10;

（2）得到p序列中[5, 10]这一段子序列s：7　　4　　8　　4　　1　　5

（3）s序列中深度最小的点即节点1就是我们要找的节点7和节点5的LCA。

例子：最近公共祖先·三

描述

上上回说到，小Hi和小Ho使用了Tarjan算法来优化了他们的“最近公共祖先”网站，但是很快这样一个离线算法就出现了问题：如果只有一个人提出了询问，那么小Hi和小Ho很难决定到底是针对这个询问就直接进行计算还是等待一定数量的询问一起计算。毕竟无论是一个询问还是很多个询问，使用离线算法都是只需要做一次深度优先搜索就可以了的。

那么问题就来了，如果每次计算都只针对一个询问进行的话，那么这样的算法事实上还不如使用最开始的朴素算法呢！但是如果每次要等上很多人一起的话，因为说不准什么时候才能够凑够人——所以事实上有可能要等上很久很久才能够进行一次计算，实际上也是很慢的！

“那到底要怎么办呢？在等到10分钟，或者凑够一定数量的人两个条件满足一个时就进行运算？”小Ho想出了一个折衷的办法。

“哪有这么麻烦！别忘了和离线算法相对应的可是有一个叫做在线算法的东西呢！”小Hi笑道。

小Ho面临的问题还是和之前一样：假设现在小Ho现在知道了N对父子关系——父亲和儿子的名字，并且这N对父子关系中涉及的所有人都拥有一个共同的祖先（这个祖先出现在这N对父子关系中），他需要对于小Hi的若干次提问——每次提问为两个人的名字（这两个人的名字在之前的父子关系中出现过），告诉小Hi这两个人的所有共同祖先中辈分最低的一个是谁？

提示：最近公共祖先无非就是两点连通路径上高度最小的点嘛！

输入

每个测试点（输入文件）有且仅有一组测试数据。

每组测试数据的第1行为一个整数N，意义如前文所述。

每组测试数据的第2~N+1行，每行分别描述一对父子关系，其中第i+1行为两个由大小写字母组成的字符串Father_i, Son_i，分别表示父亲的名字和儿子的名字。

每组测试数据的第N+2行为一个整数M，表示小Hi总共询问的次数。

每组测试数据的第N+3~N+M+2行，每行分别描述一个询问，其中第N+i+2行为两个由大小写字母组成的字符串Name1_i, Name2_i，分别表示小Hi询问中的两个名字。

对于100%的数据，满足N<=10^5，M<=10^5, 且数据中所有涉及的人物中不存在两个名字相同的人（即姓名唯一的确定了一个人），所有询问中出现过的名字均在之前所描述的N对父子关系中出现过，且每个输入文件中第一个出现的名字所确定的人是其他所有人的公共祖先。

输出

对于每组测试数据，对于每个小Hi的询问，按照在输入中出现的顺序，各输出一行，表示查询的结果：他们的所有共同祖先中辈分最低的一个人的名字。

样例输入

4
Adam Sam
Sam Joey
Sam Micheal
Adam Kevin
3
Sam Sam
Adam Sam
Micheal Kevin

样例输出

Sam
Adam
Adam

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include <iostream>
#include <string>
#include <vector>
#include <queue>
#include <map>
#include <algorithm>

using namespace std;

const int maxn = 200009;
const int maxl = 21;

map <string, int> rn;
vector <int> e[maxn];
string name[maxn];
int n, m, tn, ath[maxn][maxl], d[maxn];

int getNum(string n) {
	map <string, int> :: iterator i = rn. find(n);
	if (i == rn. end()) {
		name[++ tn] = n;
		rn. insert(pair<string, int> (n, tn));
		return tn;
	}
	else
		return i-> second;
}

void buildTree() {
	queue <int> q;
	int p0 = 1;
	while (ath[p0][0])
		p0 = ath[p0][0];
	d[p0] = 1;
	q. push(p0);
	while (!q. empty()) {
		int p = q. front();
		q. pop();
		for (int i = 1; i < maxl; ++ i)
			ath[p][i] = ath[ath[p][i - 1]][i - 1];
		for (vector <int> :: iterator i = e[p]. begin(); i != e[p]. end(); ++ i) {
			q. push(*i);
			d[*i] = d[p] + 1;
		}
	}
}

int LCA(int p, int q) {
	if (d[p] < d[q])
		swap(p, q);
	for (int i = maxl - 1; i >= 0; -- i)
		if (d[ath[p][i]] >= d[q])
			p = ath[p][i];
	if (p == q)
		return p;
	for (int i = maxl - 1; i >= 0; -- i)
		if (ath[p][i] ^ ath[q][i])
			p = ath[p][i], q = ath[q][i];
	return ath[p][0];
}

int main() {
	cin. sync_with_stdio(0);
	cin >> n;
	tn = 0;
	while (n --) {
		string a, b;
		cin >> a >> b;
		int na = getNum(a), nb = getNum(b);
		ath[nb][0] = na;
		e[na]. push_back(nb);
	}
	buildTree();
	cin >> m;
	while (m --) {
		string a, b;
		cin >> a >> b;
		int na = getNum(a), nb = getNum(b);
		cout << name[LCA(na, nb)] << endl;
	}
}

代码来自hiho一下 第十七周的排名第一参赛者laekov