算法

并查集

并查集主要是以数组的形式来记录一个森林结构，数组中存储每一个元素对应的父元素。在森林结构中，一棵树代表一个集合，树的根节点为该集合的代表。并查集主要有三中操作：MakeSet、find和Union。

MakeSet

该操作组要初始化并查集，具体代码为：

1
2
3
4
5
6
#define NODESIZE 1000
int father[NODESIZE];
void makeSet(int size){   //初始的集合个数
  for(int i=0; i<size; i++)
      father[i] = i;
}

find

该操作用来查找一个元素所在集合的代表元素。具体操作为：

1
2
3
4
5
int find(int x){
  while(father[x] != x)
      x = father[x];
  return x;
}

由于并查集只需要得到每一个元素所在的集合的代表，所以在查找的时候可以采用路劲压缩的方法，对每一个元素的father直接指向对应的代表节点，以后在查找代表节点的时候，就可以在常数时间内得到。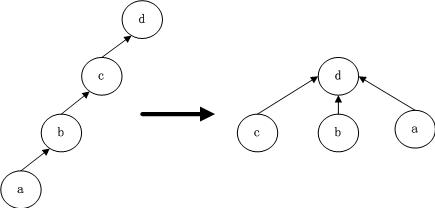
并查集之Union

1
2
3
4
5
6
7
8
9
10
11
12
//路径压缩的查找
int find(int x){
  int p = x;
  while(father[x] != x)
      x = father[x];
  while(father[p] != x){
    int temp = father[p];
      father[p] = x;
      p = temp;
    }
  return x;
}

Union

该操作主要用来合并两个集合，为了使得合并后的树高度尽量小，从而保证查找的效率，我们可以使用一个数组来记录每一棵树的高度，在合并的时候，将高度小的树合并到高度大的树。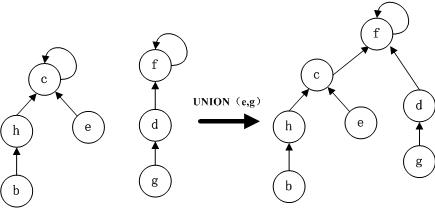
并查集之Union
具体代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
void union(int x, int y){
  //x和y处于同一个集合中，直接忽略
  if((x=find(x)) == (y=find(y))) return; //这里的对x和y的赋值，方便下面的操作，此时的x和y为其所在集合的代表
  if(rank[x] < rank[y]){
    father[x] = y;
  }
  else{
    father[y] = x;
    if(rank[y] == rank[x])
        rank[x]++;
  }

}