2016-03-19

C与C++

malloc函数的实现原理

今天看到了一个博文，感觉真的很不错，所以这里转载了一下，原文在这里。

Heap内存模型

一般来说，malloc所申请的内存主要从Heap区域分配（本文不考虑通过mmap申请大块内存的情况）。

由上文知道，进程所面对的虚拟内存地址空间，只有按页映射到物理内存地址，才能真正使用。受物理存储容量限制，整个堆虚拟内存空间不可能全部映射到实际的物理内存。Linux对堆的管理示意如下：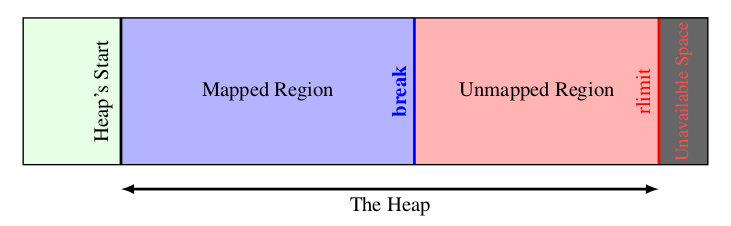

Linux维护一个break指针，这个指针指向堆空间的某个地址。从堆起始地址到break之间的地址空间为映射好的，可以供进程访问；而从break往上，是未映射的地址空间，如果访问这段空间则程序会报错。

brk与sbrk

由上文知道，要增加一个进程实际的可用堆大小，就需要将break指针向高地址移动。Linux通过brk和sbrk系统调用操作break指针。两个系统调用的原型如下：

1 2	int brk(void addr); void sbrk(intptr_t increment);

brk将break指针直接设置为某个地址，而sbrk将break从当前位置移动increment所指定的增量。brk在执行成功时返回0，否则返回-1并设置errno为ENOMEM；sbrk成功时返回break移动之前所指向的地址，否则返回(void *)-1。

一个小技巧是，如果将increment设置为0，则可以获得当前break的地址。

另外需要注意的是，由于Linux是按页进行内存映射的，所以如果break被设置为没有按页大小对齐，则系统实际上会在最后映射一个完整的页，从而实际已映射的内存空间比break指向的地方要大一些。但是使用break之后的地址是很危险的（尽管也许break之后确实有一小块可用内存地址）。

资源限制与rlimit

系统对每一个进程所分配的资源不是无限的，包括可映射的内存空间，因此每个进程有一个rlimit表示当前进程可用的资源上限。这个限制可以通过getrlimit系统调用得到，下面代码获取当前进程虚拟内存空间的rlimit：

int main() {
    struct rlimit *limit = (struct rlimit *)malloc(sizeof(struct rlimit));
    getrlimit(RLIMIT_AS, limit);
    printf("soft limit: %ld, hard limit: %ld\n", limit->rlim_cur, limit->rlim_max);
}

其中rlimit是一个结构体：

struct rlimit {
    rlim_t rlim_cur;  /* Soft limit */
    rlim_t rlim_max;  /* Hard limit (ceiling for rlim_cur) */
};

每种资源有软限制和硬限制，并且可以通过setrlimit对rlimit进行有条件设置。其中硬限制作为软限制的上限，非特权进程只能设置软限制，且不能超过硬限制。

实现malloc

####　玩具实现
在正式开始讨论malloc的实现前，我们可以利用上述知识实现一个简单但几乎没法用于真实的玩具malloc，权当对上面知识的复习：

/* 一个玩具malloc */
#include <sys/types.h>
#include <unistd.h>
void *malloc(size_t size)
{
    void *p;
    p = sbrk(0);
    if (sbrk(size) == (void *)-1)
        return NULL;
    return p;
}

这个malloc每次都在当前break的基础上增加size所指定的字节数，并将之前break的地址返回。这个malloc由于对所分配的内存缺乏记录，不便于内存释放，所以无法用于真实场景。

正式实现

下面严肃点讨论malloc的实现方案。

数据结构

首先我们要确定所采用的数据结构。一个简单可行方案是将堆内存空间以块（Block）的形式组织起来，每个块由meta区和数据区组成，meta区记录数据块的元信息（数据区大小、空闲标志位、指针等等），数据区是真实分配的内存区域，并且数据区的第一个字节地址即为malloc返回的地址。

可以用如下结构体定义一个block：

typedef struct s_block *t_block;
struct s_block {
    size_t size;  /* 数据区大小 */
    t_block next; /* 指向下个块的指针 */
    int free;     /* 是否是空闲块 */
    int padding;  /* 填充4字节，保证meta块长度为8的倍数 */
    char data[1]  /* 这是一个虚拟字段，表示数据块的第一个字节，长度不应计入meta */
};

由于我们只考虑64位机器，为了方便，我们在结构体最后填充一个int，使得结构体本身的长度为8的倍数，以便内存对齐。示意图如下：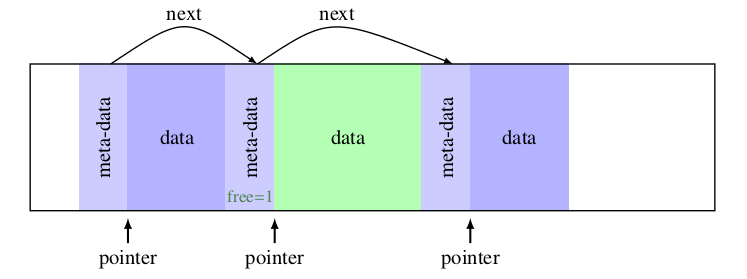

寻找合适的block

现在考虑如何在block链中查找合适的block。一般来说有两种查找算法：

First fit：从头开始，使用第一个数据区大小大于要求size的块所谓此次分配的块
Best fit：从头开始，遍历所有块，使用数据区大小大于size且差值最小的块作为此次分配的块

两种方法各有千秋，best fit具有较高的内存使用率（payload较高），而first fit具有更好的运行效率。这里我们采用first fit算法。

/* First fit */
t_block find_block(t_block *last, size_t size) {
    t_block b = first_block;
    while(b && !(b->free && b->size >= size)) {
        *last = b;
        b = b->next;
    }
    return b;
}

find_block从frist_block开始，查找第一个符合要求的block并返回block起始地址，如果找不到这返回NULL。这里在遍历时会更新一个叫last的指针，这个指针始终指向当前遍历的block。这是为了如果找不到合适的block而开辟新block使用的，具体会在接下来的一节用到。

开辟新的block

如果现有block都不能满足size的要求，则需要在链表最后开辟一个新的block。这里关键是如何只使用sbrk创建一个struct：

#define BLOCK_SIZE 24 /* 由于存在虚拟的data字段，sizeof不能正确计算meta长度，这里手工设置 */

t_block extend_heap(t_block last, size_t s) {
    t_block b;
    b = sbrk(0);
    if(sbrk(BLOCK_SIZE + s) == (void *)-1)
        return NULL;
    b->size = s;
    b->next = NULL;
    if(last)
        last->next = b;
    b->free = 0;
    return b;
}

分裂block

First fit有一个比较致命的缺点，就是可能会让很小的size占据很大的一块block，此时，为了提高payload，应该在剩余数据区足够大的情况下，将其分裂为一个新的block，示意如下：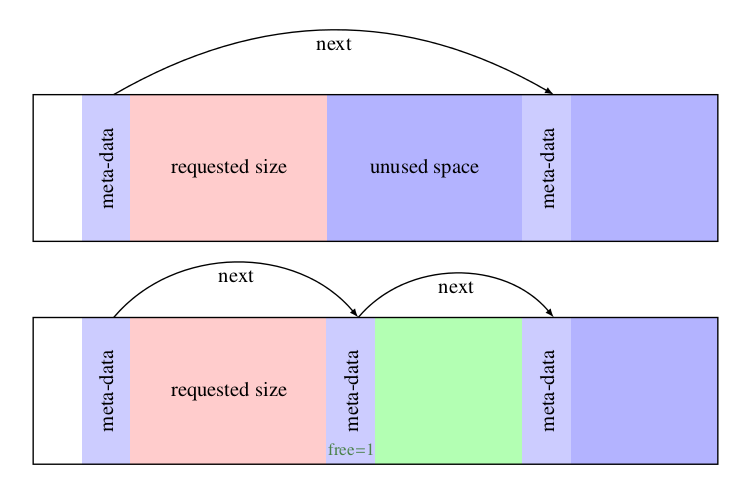

实现代码：

void split_block(t_block b, size_t s) {
    t_block new;
    new = b->data + s;
    new->size = b->size - s - BLOCK_SIZE ;
    new->next = b->next;
    new->free = 1;
    b->size = s;
    b->next = new;
}

malloc的实现

有了上面的代码，我们可以利用它们整合成一个简单但初步可用的malloc。注意首先我们要定义个block链表的头first_block，初始化为NULL；另外，我们需要剩余空间至少有BLOCK_SIZE + 8才执行分裂操作。

由于我们希望malloc分配的数据区是按8字节对齐，所以在size不为8的倍数时，我们需要将size调整为大于size的最小的8的倍数：

size_t align8(size_t s) {
    if(s & 0x7 == 0)
        return s;
    return ((s >> 3) + 1) << 3;
}

#define BLOCK_SIZE 24
void *first_block=NULL;

/* other functions... */

void *malloc(size_t size) {
    t_block b, last;
    size_t s;
    /* 对齐地址 */
    s = align8(size);
    if(first_block) {
        /* 查找合适的block */
        last = first_block;
        b = find_block(&last, s);
        if(b) {
            /* 如果可以，则分裂 */
            if ((b->size - s) >= ( BLOCK_SIZE + 8))
                split_block(b, s);
            b->free = 0;
        } else {
            /* 没有合适的block，开辟一个新的 */
            b = extend_heap(last, s);
            if(!b)
                return NULL;
        }
    } else {
        b = extend_heap(NULL, s);
        if(!b)
            return NULL;
        first_block = b;
    }
    return b->data;
}

calloc的实现

有了malloc，实现calloc只要两步：

malloc一段内存
将数据区内容置为0

由于我们的数据区是按8字节对齐的，所以为了提高效率，我们可以每8字节一组置0，而不是一个一个字节设置。我们可以通过新建一个size_t指针，将内存区域强制看做size_t类型来实现。

void *calloc(size_t number, size_t size) {
    size_t *new;
    size_t s8, i;
    new = malloc(number * size);
    if(new) {
        s8 = align8(number * size) >> 3;
        for(i = 0; i < s8; i++)
            new[i] = 0;
    }
    return new;
}

free的实现

free的实现并不像看上去那么简单，这里我们要解决两个关键问题：

如何验证所传入的地址是有效地址，即确实是通过malloc方式分配的数据区首地址
如何解决碎片问题

首先我们要保证传入free的地址是有效的，这个有效包括两方面：

地址应该在之前malloc所分配的区域内，即在first_block和当前break指针范围内
这个地址确实是之前通过我们自己的malloc分配的

第一个问题比较好解决，只要进行地址比较就可以了，关键是第二个问题。这里有两种解决方案：一是在结构体内埋一个magic number字段，free之前通过相对偏移检查特定位置的值是否为我们设置的magic number，另一种方法是在结构体内增加一个magic pointer，这个指针指向数据区的第一个字节（也就是在合法时free时传入的地址），我们在free前检查magic pointer是否指向参数所指地址。这里个人觉得可以直接根据block数据结构中的成员char data[1]来实现，不需要引入新的magic pointer？？？

这里我们采用第二种方案：

首先我们在结构体中增加magic pointer（同时要修改BLOCK_SIZE）：

typedef struct s_block *t_block;
struct s_block {
    size_t size;  /* 数据区大小 */
    t_block next; /* 指向下个块的指针 */
    int free;     /* 是否是空闲块 */
    int padding;  /* 填充4字节，保证meta块长度为8的倍数 */
    void *ptr;    /* Magic pointer，指向data */
    char data[1]  /* 这是一个虚拟字段，表示数据块的第一个字节，长度不应计入meta */
};

然后我们定义检查地址合法性的函数

t_block get_block(void *p) {
    char *tmp;  
    tmp = p;
    return (p = tmp -= BLOCK_SIZE);
}

int valid_addr(void *p) {
    if(first_block) {
        if(p > first_block && p < sbrk(0)) {
            return p == (get_block(p))->ptr;
        }
    }
    return 0;
}

当多次malloc和free后，整个内存池可能会产生很多碎片block，这些block很小，经常无法使用，甚至出现许多碎片连在一起，虽然总体能满足某此malloc要求，但是由于分割成了多个小block而无法fit，这就是碎片问题。

一个简单的解决方式时当free某个block时，如果发现它相邻的block也是free的，则将block和相邻block合并。为了满足这个实现，需要将s_block改为双向链表。修改后的block结构如下：

typedef struct s_block *t_block;
struct s_block {
    size_t size;  /* 数据区大小 */
    t_block prev; /* 指向上个块的指针 */
    t_block next; /* 指向下个块的指针 */
    int free;     /* 是否是空闲块 */
    int padding;  /* 填充4字节，保证meta块长度为8的倍数 */
    void *ptr;    /* Magic pointer，指向data */
    char data[1]  /* 这是一个虚拟字段，表示数据块的第一个字节，长度不应计入meta */
};

合并方法如下：

t_block fusion(t_block b) {
    if (b->next && b->next->free) {
        b->size += BLOCK_SIZE + b->next->size;
        b->next = b->next->next;
        if(b->next)
            b->next->prev = b;
    }
    return b;
}

有了上述方法，free的实现思路就比较清晰了：首先检查参数地址的合法性，如果不合法则不做任何事；否则，将此block的free标为1，并且在可以的情况下与后面的block进行合并。如果当前是最后一个block，则回退break指针释放进程内存，如果当前block是最后一个block，则回退break指针并设置first_block为NULL。实现如下：

void free(void *p) {
    t_block b;
    if(valid_addr(p)) {
        b = get_block(p);
        b->free = 1;
        if(b->prev && b->prev->free)
            b = fusion(b->prev);
        if(b->next)
            fusion(b);
        else {
            if(b->prev)
                b->prev->prev = NULL;
            else
                first_block = NULL;
            brk(b);
        }
    }
}

realloc的实现

为了实现realloc，我们首先要实现一个内存复制方法。如同calloc一样，为了效率，我们以8字节为单位进行复制：

void copy_block(t_block src, t_block dst) {
    size_t *sdata, *ddata;
    size_t i;
    sdata = src->ptr;
    ddata = dst->ptr;
    for(i = 0; (i * 8) < src->size && (i * 8) < dst->size; i++)
        ddata[i] = sdata[i];
}

然后我们开始实现realloc。一个简单（但是低效）的方法是malloc一段内存，然后将数据复制过去。但是我们可以做的更高效，具体可以考虑以下几个方面：

如果当前block的数据区大于等于realloc所要求的size，则不做任何操作
如果当前block的数据区不能满足size，但是其后继block是free的，并且合并后可以满足，则考虑做合并
下面是realloc的实现：

void *realloc(void *p, size_t size) {
    size_t s;
    t_block b, new;
    void *newp;
    if (!p)
        /* 根据标准库文档，当p传入NULL时，相当于调用malloc */
        return malloc(size);
    if(valid_addr(p)) {
        s = align8(size);
        b = get_block(p);
        if(b->size >= s) {
            if(b->size - s >= (BLOCK_SIZE + 8))
                split_block(b,s);
        } else {
            /* 看是否可进行合并 */
            if(b->next && b->next->free
                    && (b->size + BLOCK_SIZE + b->next->size) >= s) {
                fusion(b);
                if(b->size - s >= (BLOCK_SIZE + 8))
                    split_block(b, s);
            } else {
                /* 新malloc */
                newp = malloc (s);
                if (!newp)
                    return NULL;
                new = get_block(newp);
                copy_block(b, new);
                free(p);
                return(newp);
            }
        }
        return (p);
    }
    return NULL;
}

遗留问题和优化

以上是一个较为简陋，但是初步可用的malloc实现。还有很多遗留的可能优化点，例如：

同时兼容32位和64位系统
在分配较大快内存时，考虑使用mmap而非sbrk，这通常更高效
可以考虑维护多个链表而非单个，每个链表中的block大小均为一个范围内，例如8字节链表、16字节链表、24-32字节链表等等。此时可以根据size到对应链表中做分配，可以有效减少碎片，并提高查询block的速度
可以考虑链表中只存放free的block，而不存放已分配的block，可以减少查找block的次数，提高效率

LiuYongbin

Hey boy just do it!